03 - Quantum Confined Stark Effect
I Quantum Well mostrano una struttura a bande con numerose sottobande nella banda di conduzione e di valenza. Indichiamo i livelli della banda di conduzione come 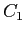 ,
,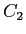 ,... e i livelli della banda di valenza (che si dividono in livelli di lacune pesanti e leggeri) come
,... e i livelli della banda di valenza (che si dividono in livelli di lacune pesanti e leggeri) come 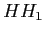 ,
,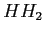 ,... e
,... e 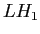 ,
,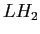 ,... . Le regole di selezione permettono solamente alcune transizioni tra i livelli, e, inoltre, rendono la forza di interazione delle transizioni generalmente differente per i fotoni polarizzati TE o TM. Il profilo di assorbimento del quantum well deriva dalla JDOS (Joint density of states), che ha la forma a gradini; tuttavia solo i gradini corrispondenti a transizioni permesse vanno considerati, e il peso di ciascuno gradino sar´┐Ż diverso a seconda della polarizzazione.
L'effetto degli eccitoni, presenti in un quantum well anche a temperatura ambiente, gioca un ruolo significativo nelle propriet´┐Ż ottiche. Tali quasi-particelle possono essere descritte come una coppia elettrone-lacuna legati dalla forza di Coulomb, e la loro energia di legame ´┐Ż pi´┐Ż grande in un quantum well che in un bulk; interagiscono con i fotoni portando a picchi di assorbimento immediatamente prima di ciascun gradino della JDOS(vedi figura 1).
,... . Le regole di selezione permettono solamente alcune transizioni tra i livelli, e, inoltre, rendono la forza di interazione delle transizioni generalmente differente per i fotoni polarizzati TE o TM. Il profilo di assorbimento del quantum well deriva dalla JDOS (Joint density of states), che ha la forma a gradini; tuttavia solo i gradini corrispondenti a transizioni permesse vanno considerati, e il peso di ciascuno gradino sar´┐Ż diverso a seconda della polarizzazione.
L'effetto degli eccitoni, presenti in un quantum well anche a temperatura ambiente, gioca un ruolo significativo nelle propriet´┐Ż ottiche. Tali quasi-particelle possono essere descritte come una coppia elettrone-lacuna legati dalla forza di Coulomb, e la loro energia di legame ´┐Ż pi´┐Ż grande in un quantum well che in un bulk; interagiscono con i fotoni portando a picchi di assorbimento immediatamente prima di ciascun gradino della JDOS(vedi figura 1).
A causa dell'effetto combinato delle regole di selezione sensibili alla polarizzazione, i quantum well mostrano gi´┐Ż, in assenza di un campo elettrico, un marcato dicroismo, cio´┐Ż un differente profilo di assorbimento e indice rifrattivo per ciascuna polarizzazione (vedi figura 1). Siccome la forza di interazione della transizione
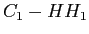 ´┐Ż nulla per la polarizzazione TM, nella risposta di assorbimento della polarizzazione TM manca il primo gradino della JDOS, mentre ´┐Ż presente il picco dell'eccitone associato.
L'applicazione di un campo esterno fa si che le bande di un quantum well si pieghino, esattamente come nel caso bulk; l'inclinazione delle bande porta a 3 effetti:
´┐Ż nulla per la polarizzazione TM, nella risposta di assorbimento della polarizzazione TM manca il primo gradino della JDOS, mentre ´┐Ż presente il picco dell'eccitone associato.
L'applicazione di un campo esterno fa si che le bande di un quantum well si pieghino, esattamente come nel caso bulk; l'inclinazione delle bande porta a 3 effetti:
- I livelli energetici coinvolti nelle transizioni si avvicinano, a causa dello spostamento nel profilo di potenziale del quantum well (vedi figura 2 per un esempio riferito alla transizione
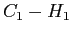 , dove
, dove 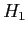 indica
indica 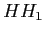 o
o 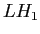 in base all'ordine delle sottobande, che pu´┐Ż variare nei QW sotto stress strutturale). Di conseguenza l'assorbimento pu´┐Ż avvenire a energie pi´┐Ż basse, si ha cio´┐Ż uno spostamento verso il rosso.
in base all'ordine delle sottobande, che pu´┐Ż variare nei QW sotto stress strutturale). Di conseguenza l'assorbimento pu´┐Ż avvenire a energie pi´┐Ż basse, si ha cio´┐Ż uno spostamento verso il rosso.
- Il livello degli eccitoni subisce uno spostamento in energia.
- La funzione di inviluppo degli stati della banda di conduzione e di valenza cambia, portando a una modulazione della forza di interazione di transizione. Per campi molto grandi ci aspettiamo che la forza di interazione decresca, a causa della decrescente sovrapposizione tra le due funzioni d'onda.
Possiamo esprimere l'energia del fotone come:
dove
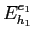
´┐Ż la differenza di energia tra i livelli
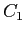
e
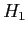
,
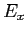
´┐Ż l'energia di legame dell'eccitone (dell'ordine dei 10 meV). L'energia di transizione intersottobanda pu´┐Ż essere scomposta come:
dove
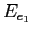
´┐Ż il livello di
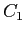
sopra al limite della banda di conduzione,
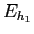
´┐Ż il livello di
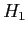
sotto al limite della banda di valenza
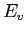
(
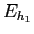
) ´┐Ż perci´┐Ż negativo.
Si pu´┐Ż dimostrare che l'energia di transizione decresce con il campo applicato secondo una legge quadratica:
dove 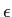 ´┐Ż il campo applicato, L ´┐Ż lo spessore effettivo del quantum well e
´┐Ż il campo applicato, L ´┐Ż lo spessore effettivo del quantum well e
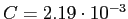 ´┐Ż una costante adimensionata. Un esempio dello spostamento dell'energia per un quantum well di 9.5nm in GaAs/AlGaAs ´┐Ż mostrato in figura 3.
´┐Ż una costante adimensionata. Un esempio dello spostamento dell'energia per un quantum well di 9.5nm in GaAs/AlGaAs ´┐Ż mostrato in figura 3.
Figura 3:
Spostamento livelli sottobande
|
|
Per campi applicati dell'ordine di 100 kV/cm, corrispondenti a una differenza di potenziale
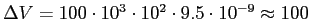
mV attraverso il Quantum Well, lo spostamento ´┐Ż dell'ordine di 10meV. Un secondo contributo allo spostamento del limite di assorbimento ´┐Ż causato dal cambiamento dell'energia di legame dell'eccitone (vedere figura
4 per un esempio riferito a un QW in GaAs). Per aumentare il campo applicato l'energia di legame decresce leggermente, cio´┐Ż gli eccitoni si avvicinano ai livelli dell'energia di stato; ci´┐Ż parzialmente compensa lo spostamento dei livelli di energia, ma, per QW sottili, la variazione ´┐Ż circa un ordine di grandezza pi´┐Ż piccola di
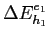
.
Figura 4:
Spostamento lacune pesanti e leggere
|
|
Consideriamo ora l'effetto complessivo risultante dall'applicazione di un campo elettrico. Siccome le tipiche strutture dei QW sono giunzioni PiN, la tensione applicata fa si che la giunzione sia polarizzata inversamente (esattamente come in un diodo PiN). Il campo risultante quasi uniforme nella regione intrinseca diminuisce l'energia di transizione intersottobanda e l'ampiezza dell'energia di legame dell'eccitone (a causa della diminuzione della forza di Coulomb tra elettrone e lacuna). Come risultato finale lo spettro di assorbimento ´┐Ż spostato verso lunghezze d'onda pi´┐Ż lunghe (red shift). Aumentando il campo applicato, osserviamo anche la scomparsa del picco di assorbimento alla risonanza dell'eccitone a causa della diminuzione della sovrapposizione di elettroni e lacune; la diminuzione dipende dalla forza di confinamento dei portatori nel pozzo. Le variazioni del profilo di assorbimento sono infine influenzate dalla differente forza di interazione delle transizioni tra i livelli di lacune leggere e pesanti nella banda di valenza e tra i livelli degli elettroni nella banda di conduzione. Ricordiamo che le forze previste:
- Per la polarizzazione TE,
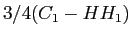 ,
,
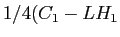
- Per la polarizzazione TM,
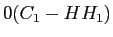 ,
,
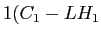
Un esempio di spettro normalizzato di assorbimento (inteso come la trasmissione del materiale in scala logaritmica) ´┐Ż mostrato in figura 5; il Dicroismo esiste anche in presenza di campo applicato, e sono visibili l'effetto dei picchi di risonanza di assorbimento dell'eccitone e la loro riduzione all'aumentare del campo elettrico. A causa dei picchi degli eccitoni grandi variazioni di assorbimento possono essere ottenuti a campi relativamente bassi ma solo in una gamma molto stretta di lunghezze d'onda.
Figura 5:
Spettro assorbimento TE e TM
|
|
Il dicroismo pu´┐Ż essere una limitazione negli EAM, almeno nei dispositivi discreti, dato che richiede la luce entrante sia polarizzata in uno specifico stato TE o TM. Dispositivi insensibili alla polarizzazione possono essere sviluppati rimuovendo il Dicroismo attraverso l'uso di QW sottoposti a stress meccanico.
in presenza di uno stress applicato la struttura a bande del QW(come nella struttura a bande bulk) si modifica in due modi: stress di compressione o di tensione portano a diminuire o aumentare la costante reticolare, e perci´┐Ż ad aumentare e diminuire l'Eg; lo stress fa si, in un bulk che lacune pesante e leggere perdano la loro degenerazione, mentre in un QW fa si che cambi l'allineamento relativo dei livelli di lacune pesanti e leggere. Come risultato abbiamo una situazione mostrata in figura 6; uno stress tensile pu´┐Ż portare all'allineamento delle energie 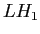 e
e 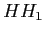 ; grazie al quale viene eliminata, o per lo meno ridotta, l'anisotropia della polarizzazione. L'introduzione di uno stress di tensione nel pozzo limita lo spessore totale del MQW; comunque, questo effetto pu´┐Ż essere compensato utilizzando una barriera con stress di compressione.
; grazie al quale viene eliminata, o per lo meno ridotta, l'anisotropia della polarizzazione. L'introduzione di uno stress di tensione nel pozzo limita lo spessore totale del MQW; comunque, questo effetto pu´┐Ż essere compensato utilizzando una barriera con stress di compressione.
Figura 6:
Stress meccanico
|
|
Un ultimo effetto riguarda la dipendenza del profilo di assorbimento dalla densit´┐Ż di portatori. Idealmente, gli EAM operano con densit´┐Ż di portatori quasi nulla: si suppone che la banda di conduzione sia vuota, e il campo elettrico sia uniforme e non perturbato dagli effetti della carica spaziale. Comunque i portatori foto-generati si ricombinano o sono eliminati dalla regione non drogata di assorbimento con un tempo di vita medio
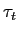
, che pu´┐Ż essere considerato come un tempo di transito o di scomparsa. Considerando che i foto-portatori sono generati da un assorbimento di un fotone, e hanno tempo di vita
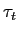
abbiamo dalla equazione di continuit´┐Ż di flusso dei fotoni in condizioni DC:
dove
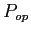
´┐Ż la potenza ottica incidente e A la sezione trasversale del dispositivo. La densit´┐Ż dei portatori risultante ´┐Ż dunque:
Aumentando la potenza ottica la densit´┐Ż di portatori nella regione di assorbimento aumenta. Al di la di un certo livello, si pu´┐Ż verificare la saturazione di potenza ottica a causa di due effetti: primo, il foto-portatori generati schermano il campo esterno a RF applicato, portando cos´┐Ż ad una diminuzione dell'assorbimento; secondo, l'emissione inizia a giocare un ruolo importante a causa del riempimento delle bande contrapponendosi cos´┐Ż all'effetto dell'assorbimento. A causa di entrambi gli effetti l'assorbimento diminuir´┐Ż all'aumentare della potenza ottica. I meccanismi che limitano il tempo di scomparsa
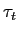
sono nei modulatori bulk, l'intrappolamento della carica alla eterogiunzione (ad esempio InGaAsP-InP); nei QW l'accumulazione di lacune nel pozzo (a causa della loro massa maggiore). E' necessario il dimensionamento del band gap per ridurre l'elevato offset delle bande e
notiamo che lo stesso problema si verifica nei fotodiodi dove tuttavia la potenza ottica in ingresso ´┐Ż bassa abbastanza da rendere l'effetto di saturazione meno significativo.